Aturan Penjumlahan dan Pengurangan Bilangan Bulat
A. Penjumlahan
Di SD pasti sudah sangat paham bagaimanan menjumlahkan suatu bilangan bulat bukan. Ada beberapa 2 teknik yang dapat kalian gunakan, yaitu menggunakan garis bilangan dan sistem utang dan menabung.
Dengan menggunakan garis bilangan disepakati bahwa bilangan bulat + artinya maju sedangkan bilangan bulat negatif artinya mundur.
Contoh :
Hitunglah hasil penjumlahan
a. 6 dan 2
b. 2 dan – 8
Jawab :
a. Penjumlahan 6 dan 2
6 dan 2 adalah bilangan bulat positif yang artinya kita akan maju sebanyak 6 + 2 langkah. Yang perlu diingan selalu mulai dari angka 0 ya!
b. Penjumlahan 2 dan – 8
Jika menggunakan sistem hutang dan menabung disepakati bahwa bilangan bulat positif artinya menabung sedangkan bilangan bulat negatif artinya hutang.
Contoh :
Hitunglah hasil penjumlahan
a. 2 + 4
b. – 9 + 5
Jawab :
a. 2 + 4 artinya kita menambung sebanyak dua, kemudian menabung lagi sebanyak 4 maka jumlah tabungan kita adalah : 2 + 4 = 6
b. – 9 + 5 artinya kita punya hutang 9 dan akan kita bayar dengan tabungan 5, maka hutang kita tentu belum lunas. Jumlah sisa hutang adalah : - 9 + 5 = -4
Jika yang dijumlahkan adalah :
1. Bilangan positif + bilangan positif = bilangan positif. Contoh : 1 + 2 = 3
2. Bilangan negatif + bilangan negatif = bilangan negatif. Contoh : -4 + (-6) = - 10
3. Bilangan positif + bilangan negatif = hasilnya tergantung bilangan mana yang paling besar.
Jika bil positif > bil negatif = bil positif. Contoh : 8 + (-6) = 2
Jika bil positif < bil negatif = bil negatif. Contoh : -7 + 3 = - 4
Tentunya kalian sudah sangat mahir menjumlahkan bilangan bulat bukan!
Penjumlahan bilangan bulat itu memiliki beberapa sifat yaitu sebagai berikut :
1. 2 + 3 = 5 dan 3 + 2 = 5
Artinya 2 + 3 = 3 + 2 = 5
Sifat ini disebut dengan sifat komutatif (pertukaran) dimana secara umum dituliskan sebagai berikut :
Jika a dan b adalah dua buah bilangan bulat, maka berlaku a + b = b + a
2. 1 + 2 + 3 = 6
( 1 + 2 ) + 3 = 3 + 3 = 6
1 + (2 + 3 ) = 1 + 5 = 6
Artinya ( 1 + 2 ) + 3 = 1 + (2 + 3 ) = 6. Sifat ini disebut dengan sifat asosiatif (pengelompokkan) yang secara umum dapat ditulis sebagai berikut :
Jika a, b dan c adalah bilangan bulat maka berlaku (a + b) + c = a + (b + c)
3. Sifat tertutup
4 + 5 = 9
4, 5 dan 9 adalah sama – sama bilangan bulat. Artinya jika dua atau lebih bilangan bulat dijumlahkan, maka hasilnya pasti adalah sebuah bilangan bulat. Sifat ini disebut dengan sifat tertutup.
4. Sifat identitas
Bilangan yang menyatakan identitas bilangan lain adalah 0. Jika suatu bilngan bulat ditambah dengan 0, maka hasilnya adalah bilangan bulat itu sendiri.
Contoh :
2 + 0 = 2
-7 + 0 = -7
5. Invers
Invers maksudnya adalah lawan dari suatu bilangan. Bilangan bulat positif lawannya adalah bilangan bulat negatif dengan jarak kedua bilangan ke titik 0 adalah sama.
Contoh :
Lawan atau invers dari -5 adalah 5.
B. Pengurangan
Tak berbeda jauh dengan penjumlahan, pengurangan bilangan bulat juga bisa dicari menggunakan garis bilangan.
Contoh :
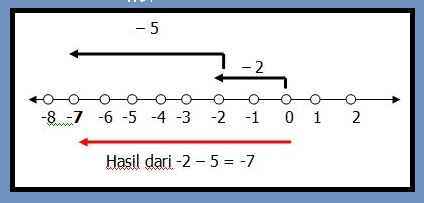
Tentukanlah hasil penjumlahan dari – 2 – 5!
Jawab :
Untuk pengurangan, tanda kurang didepan angka menjadi milik nya. Jadi angka 5 pada doal diatas memiliki tanda negatif. Artinya untuk mencari hasil pengurangan – 2 – 5 kita akan mundur sejauh 2 dan 5 satuan.
Jika bilangan bulat yang dikurangkan adalah :
1. Bilangan bulat positif – bilangan bulat positif = tergantung pada bilangan bulat mana yang lebih besar. Jika yang pertama lebih besar dari yang kedua, maka hasilnya adalah +, sedangkan jika pertama lebih kecil dari yang kedua maka hasilnya adalah -.
Contoh :
8 – 5 = 3 (karena 8 > 5)
5 – 8 = - 3 (karena 5 < 8)
2. Bilangan bulat positif – bilangan bulat negatif = bilangan bulat positif
Contoh :
8 – ( - 2 ) = 8 + 2 = 10
Secara umum jika a - (-b) = a + b
3. Bilangan bulat negatif – bilangan bulat positif = bilangan bulat negatif
Contoh :
- 2 – 3 = - 5
4. Bilangan bulat negatif – bilangan bulat negatif = tergantung pada bilangan mana yang lebih besar.
Contoh :
Jika bilangan negatif pertama lebih besar = -
- 9 – ( - 6) = - 9 + 6 = - 3
Jika bilangan negatif pertama lebih kecil = +
- 6 – ( - 8 ) = - 6 + 8 = 2
Secara umum pengurangan dua bilangan bulat dapat kita tulis sebagai berikut :
1. a – b = a + (- b)
2. a – (- b) = a + b
3. – a – ( - b) = - a + b
4. – a – b = - a + ( - b)
Pada pengurangan tidak belaku sifat komutatif dan asosiatif.
Contoh :
2 – 3 = -1 tidak sama dengan 3 – 2 = 1 (tidak berlaku sifat komutatif)
(2 – 3 ) – 4 = - 1 – 5 = - 5 tidak sama dengan 2 – (3 – 4) = 2 – ( - 1) = 2 (tidak berlaku sifat asosiatif.
Penjumlahan dan pengurangan jika ada tanda kurung ()
Tanda kurung merupakan perintah kerjakanlah terlebih dahulu.
Contoh :
1. ( - 7 + 14 ) + ( - 12) = . . . .
Kerjakan dulu hasil penjumlahan – 7 + 14 kemudian baru hasilnya dijumlahkan dengan – 12.
( - 7 + 14 ) + ( - 12) = 7 + (-12) = - 5
2. 15 + ( - 3 + 19) = 15 + 16 = 31
Di SD pasti sudah sangat paham bagaimanan menjumlahkan suatu bilangan bulat bukan. Ada beberapa 2 teknik yang dapat kalian gunakan, yaitu menggunakan garis bilangan dan sistem utang dan menabung.
Dengan menggunakan garis bilangan disepakati bahwa bilangan bulat + artinya maju sedangkan bilangan bulat negatif artinya mundur.
Contoh :
Hitunglah hasil penjumlahan
a. 6 dan 2
b. 2 dan – 8
Jawab :
a. Penjumlahan 6 dan 2
6 dan 2 adalah bilangan bulat positif yang artinya kita akan maju sebanyak 6 + 2 langkah. Yang perlu diingan selalu mulai dari angka 0 ya!
b. Penjumlahan 2 dan – 8
Jika menggunakan sistem hutang dan menabung disepakati bahwa bilangan bulat positif artinya menabung sedangkan bilangan bulat negatif artinya hutang.
Contoh :
Hitunglah hasil penjumlahan
a. 2 + 4
b. – 9 + 5
Jawab :
a. 2 + 4 artinya kita menambung sebanyak dua, kemudian menabung lagi sebanyak 4 maka jumlah tabungan kita adalah : 2 + 4 = 6
b. – 9 + 5 artinya kita punya hutang 9 dan akan kita bayar dengan tabungan 5, maka hutang kita tentu belum lunas. Jumlah sisa hutang adalah : - 9 + 5 = -4
Jika yang dijumlahkan adalah :
1. Bilangan positif + bilangan positif = bilangan positif. Contoh : 1 + 2 = 3
2. Bilangan negatif + bilangan negatif = bilangan negatif. Contoh : -4 + (-6) = - 10
3. Bilangan positif + bilangan negatif = hasilnya tergantung bilangan mana yang paling besar.
Jika bil positif > bil negatif = bil positif. Contoh : 8 + (-6) = 2
Jika bil positif < bil negatif = bil negatif. Contoh : -7 + 3 = - 4
Tentunya kalian sudah sangat mahir menjumlahkan bilangan bulat bukan!
Penjumlahan bilangan bulat itu memiliki beberapa sifat yaitu sebagai berikut :
1. 2 + 3 = 5 dan 3 + 2 = 5
Artinya 2 + 3 = 3 + 2 = 5
Sifat ini disebut dengan sifat komutatif (pertukaran) dimana secara umum dituliskan sebagai berikut :
Jika a dan b adalah dua buah bilangan bulat, maka berlaku a + b = b + a
2. 1 + 2 + 3 = 6
( 1 + 2 ) + 3 = 3 + 3 = 6
1 + (2 + 3 ) = 1 + 5 = 6
Artinya ( 1 + 2 ) + 3 = 1 + (2 + 3 ) = 6. Sifat ini disebut dengan sifat asosiatif (pengelompokkan) yang secara umum dapat ditulis sebagai berikut :
Jika a, b dan c adalah bilangan bulat maka berlaku (a + b) + c = a + (b + c)
3. Sifat tertutup
4 + 5 = 9
4, 5 dan 9 adalah sama – sama bilangan bulat. Artinya jika dua atau lebih bilangan bulat dijumlahkan, maka hasilnya pasti adalah sebuah bilangan bulat. Sifat ini disebut dengan sifat tertutup.
4. Sifat identitas
Bilangan yang menyatakan identitas bilangan lain adalah 0. Jika suatu bilngan bulat ditambah dengan 0, maka hasilnya adalah bilangan bulat itu sendiri.
Contoh :
2 + 0 = 2
-7 + 0 = -7
5. Invers
Invers maksudnya adalah lawan dari suatu bilangan. Bilangan bulat positif lawannya adalah bilangan bulat negatif dengan jarak kedua bilangan ke titik 0 adalah sama.
Contoh :
Lawan atau invers dari -5 adalah 5.
B. Pengurangan
Tak berbeda jauh dengan penjumlahan, pengurangan bilangan bulat juga bisa dicari menggunakan garis bilangan.
Contoh :
Tentukanlah hasil penjumlahan dari – 2 – 5!
Jawab :
Untuk pengurangan, tanda kurang didepan angka menjadi milik nya. Jadi angka 5 pada doal diatas memiliki tanda negatif. Artinya untuk mencari hasil pengurangan – 2 – 5 kita akan mundur sejauh 2 dan 5 satuan.
Jika bilangan bulat yang dikurangkan adalah :
1. Bilangan bulat positif – bilangan bulat positif = tergantung pada bilangan bulat mana yang lebih besar. Jika yang pertama lebih besar dari yang kedua, maka hasilnya adalah +, sedangkan jika pertama lebih kecil dari yang kedua maka hasilnya adalah -.
Contoh :
8 – 5 = 3 (karena 8 > 5)
5 – 8 = - 3 (karena 5 < 8)
2. Bilangan bulat positif – bilangan bulat negatif = bilangan bulat positif
Contoh :
8 – ( - 2 ) = 8 + 2 = 10
Secara umum jika a - (-b) = a + b
3. Bilangan bulat negatif – bilangan bulat positif = bilangan bulat negatif
Contoh :
- 2 – 3 = - 5
4. Bilangan bulat negatif – bilangan bulat negatif = tergantung pada bilangan mana yang lebih besar.
Contoh :
Jika bilangan negatif pertama lebih besar = -
- 9 – ( - 6) = - 9 + 6 = - 3
Jika bilangan negatif pertama lebih kecil = +
- 6 – ( - 8 ) = - 6 + 8 = 2
Secara umum pengurangan dua bilangan bulat dapat kita tulis sebagai berikut :
1. a – b = a + (- b)
2. a – (- b) = a + b
3. – a – ( - b) = - a + b
4. – a – b = - a + ( - b)
Pada pengurangan tidak belaku sifat komutatif dan asosiatif.
Contoh :
2 – 3 = -1 tidak sama dengan 3 – 2 = 1 (tidak berlaku sifat komutatif)
(2 – 3 ) – 4 = - 1 – 5 = - 5 tidak sama dengan 2 – (3 – 4) = 2 – ( - 1) = 2 (tidak berlaku sifat asosiatif.
Penjumlahan dan pengurangan jika ada tanda kurung ()
Tanda kurung merupakan perintah kerjakanlah terlebih dahulu.
Contoh :
1. ( - 7 + 14 ) + ( - 12) = . . . .
Kerjakan dulu hasil penjumlahan – 7 + 14 kemudian baru hasilnya dijumlahkan dengan – 12.
( - 7 + 14 ) + ( - 12) = 7 + (-12) = - 5
2. 15 + ( - 3 + 19) = 15 + 16 = 31


Posting Komentar untuk "Aturan Penjumlahan dan Pengurangan Bilangan Bulat"