Tutorial Menjawab Soal Matematika Kelas 9 SMP - Aturan Dasar Bilangan Berpangkat
Soal 1 : Menyatakan perkalian berulang dalam bentuk perpangkatan
Nyatakan suatu perkalian berikut dalam bentuk perpangkatan
a. (-3) x (-3) x (-3)
b. (-3/4) x (-3/4) x (-3/4) x (-3/4)
c. t x t x t x 3 x 3 x 3
d. t x y x t x y x t
e. (1/5) x (1/5) x (1/5) x (1/5) x (1/5)
Jawab :
Jika suatu perkalian mengandung angka – angka yang berulang, maka kita bisa menulis operasi perkalian itu dalam bentuk perpangkatan.
Contoh :
a x a x a x a x a = a^5 (dibaca a pangkat 5)
Angka 5 menyatakan jumlah perkalian berulang dari a.
a. (-3) x (-3) x (-3) = (-3)^3
b. (-3/4) x (-3/4) x (-3/4) x (-3/4) = (-3/4)^4
c. t x t x t x 3 x 3 x 3 = t^3 x 3^3
(catatan : yang bisa di buat menjadi bentuk perpangkatan hanya jika angkanya sama)
d. t x y x t x y x t = t^3 x y^2
e. (1/5) x (1/5) x (1/5) x (1/5) x (1/5) = (1/5) ^4
Soal 2 : Menyatakan bentuk perpangkatan menjadi perkalian berulang bilangan
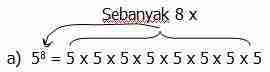
a. 5^8
b. (0,62)^4
c. P^5
d. (-1/6)^3
e. – (1/6)^3
Jawab :
Ini kebalikan soal yang pertama ya! Jadi kita akan mengubah bentuki berpangkat ke bentuk perkalian berulang. Caranya sangat mudah yaitu tinggal buat perkalian angka sebanyak pangkatnya.
b. (0,62)^4 = (0,62) x (0,62) x (0,62) x (0,62) x (0,62)
Atau kita bisa ubah dan sederhanakan bentuk desimal 0,62 menjadi pecahan biasa.
0,62 = 62/100 = 31/50
Maka (0,62)4 = (31/50)4 = (31/50) x (31/50) x (31/50) x (31/50)
b. p^5 = p x p x p x p x p
c. (-1/6)^3 = (-1/6) x (-1/6) x (-1/6)
d. – (1/6)^3 = - ((1/6) x (1/6) x (1/6))
Yang dipangkatkan pada soal diatas hanyalah 1/6 nya saja, jadi tanda – nya tidak ikut.
Soal 3 : Menentukan hasil perpangkatan suatu bilangan
a. 3^5
b. 7^3
c. 110^0
d. (0,03)^2
e. (- 1/5)^4
f. 〖-( 1/5)〗^4
Jawab :
a. 35 = 3 x 3 x 3 x 3 x 3 = 243
b. 73 = 7 x 7 x 7 = 343
c. 110^0 = 1
Salah satu difat perpangkatan adalah perpangkatan bilangan satu. Berapapun dipangkatkan, maka hasilnya akan tetap 1.
d. (0,03)^2
Pertama kita ubah dulu bentuk 0,03 menjadi bilangan berpangkat.
0,03 = 3 x 10-2 (dua angka di belakang koma)
b. (1/5)^4
Soal 4 : Menyatakan bentuk perpangkatan dengan basis 10
Nyatakanlah bilangan berikut dalam perpangkatan dengan basis 10
a. 1.000
b. 100.000
c. 1.000.000
d. 10.000.000
Jawab :
Caranya adalah dengan menghitung jumlah nolnya dan jadikan itu pangkat bilangan basi 10 nya.
a. 1.000 = 10^3
b. 100.000 = 10^5
c. 1.000.000 = 10^6
d. 10.000.000 = 10^7
Soal 5
Nyatakan bilangan berikut dalam perpangkatan dengan basir 2
a. 256
b. 64
c. 512
d. 1.048.576
Jawab :
Caranya adalah dengan mengubah angka – angka diatas menjadi perkalian berulang 2, kemudian baru kita buat bilangan perpangkatannya.
a. 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 28
b. 64 = 2 x 2 x 2 x 2 x 2 x 2 = 26
c. 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 29
d. 1.048.576 = 512 x 512 x 4 = 29 x 29 x 22 = 29 + 9 + 2 = 220
Soal 6 :Menentukan operasi campuran bilangan berpangkat
Tentukanlah hasil dari operasi berikut ini.
a. 5 + (3 x 2^4)
b. ½ (6^3 – 4^2)
c. 8 + (3 x (-3)^4)
d. (6^4 – 4^4) : 2
e. (1/4)^4 x (-1/3)^2
Jawab :
Yang perlu kalian ingat dalam aturan operasi bilangan adalah operasi mana yang dikerjakan terlebih dahulu. Urutannya adalah sebagai berikut:
1. Dalam kurung
2. Akar dan pangkat
3. Kali dan bagi
4. Tambah dan kurang
a. 5 + 3 x 2^4 = 5 + 3 x 16 = 5 + 48 = 53
b. ½ (6^3 – 4^2) = ½ (216 – 8) = ½ (208) = 104
c. 8 + 3 x (-3)^4 = 8 x 3 x 81 = 1944
d. (6^4 – 4^4) : 2 = (1296 – 256) : 2 = 1040 : 2 = 520
e. (1/4)^4 x (-1/3)^2 = (1/4^4 ) x (1/3^2 ) = 1/256 x 1/9 = 1/2304
Soal 8 : Menentukan pangkat yang sesuai dari suatu persamaan bilangan berpangkat
a. 7^x = 343
b. 2^x = 64
c. 10^x = 10.000
d. 5^x = 625
Jawab :
Jika :
a^x = a^y maka x = y
Contoh : 2^x = 8, berapa nilai x?
Jawab : 2^x = 2^3 ==> maka x = 3
a. 7^x = 343 ==> 7^x = 73 ==> x = 3
b. 2^x = 64 ==> 2^x = 26 ==> x = 6
c. 10^x = 10.000 ==> 10^x = 104 ==> x = 4
d. 5^x = 625 ==> 5^x = 54 ==> x = 4
Nyatakan suatu perkalian berikut dalam bentuk perpangkatan
a. (-3) x (-3) x (-3)
b. (-3/4) x (-3/4) x (-3/4) x (-3/4)
c. t x t x t x 3 x 3 x 3
d. t x y x t x y x t
e. (1/5) x (1/5) x (1/5) x (1/5) x (1/5)
Jawab :
Jika suatu perkalian mengandung angka – angka yang berulang, maka kita bisa menulis operasi perkalian itu dalam bentuk perpangkatan.
Contoh :
a x a x a x a x a = a^5 (dibaca a pangkat 5)
Angka 5 menyatakan jumlah perkalian berulang dari a.
a. (-3) x (-3) x (-3) = (-3)^3
b. (-3/4) x (-3/4) x (-3/4) x (-3/4) = (-3/4)^4
c. t x t x t x 3 x 3 x 3 = t^3 x 3^3
(catatan : yang bisa di buat menjadi bentuk perpangkatan hanya jika angkanya sama)
d. t x y x t x y x t = t^3 x y^2
e. (1/5) x (1/5) x (1/5) x (1/5) x (1/5) = (1/5) ^4
Soal 2 : Menyatakan bentuk perpangkatan menjadi perkalian berulang bilangan
a. 5^8
b. (0,62)^4
c. P^5
d. (-1/6)^3
e. – (1/6)^3
Jawab :
Ini kebalikan soal yang pertama ya! Jadi kita akan mengubah bentuki berpangkat ke bentuk perkalian berulang. Caranya sangat mudah yaitu tinggal buat perkalian angka sebanyak pangkatnya.
b. (0,62)^4 = (0,62) x (0,62) x (0,62) x (0,62) x (0,62)
Atau kita bisa ubah dan sederhanakan bentuk desimal 0,62 menjadi pecahan biasa.
0,62 = 62/100 = 31/50
Maka (0,62)4 = (31/50)4 = (31/50) x (31/50) x (31/50) x (31/50)
b. p^5 = p x p x p x p x p
c. (-1/6)^3 = (-1/6) x (-1/6) x (-1/6)
d. – (1/6)^3 = - ((1/6) x (1/6) x (1/6))
Yang dipangkatkan pada soal diatas hanyalah 1/6 nya saja, jadi tanda – nya tidak ikut.
Soal 3 : Menentukan hasil perpangkatan suatu bilangan
a. 3^5
b. 7^3
c. 110^0
d. (0,03)^2
e. (- 1/5)^4
f. 〖-( 1/5)〗^4
Jawab :
a. 35 = 3 x 3 x 3 x 3 x 3 = 243
b. 73 = 7 x 7 x 7 = 343
c. 110^0 = 1
Salah satu difat perpangkatan adalah perpangkatan bilangan satu. Berapapun dipangkatkan, maka hasilnya akan tetap 1.
d. (0,03)^2
Pertama kita ubah dulu bentuk 0,03 menjadi bilangan berpangkat.
0,03 = 3 x 10-2 (dua angka di belakang koma)
b. (1/5)^4
Soal 4 : Menyatakan bentuk perpangkatan dengan basis 10
Nyatakanlah bilangan berikut dalam perpangkatan dengan basis 10
a. 1.000
b. 100.000
c. 1.000.000
d. 10.000.000
Jawab :
Caranya adalah dengan menghitung jumlah nolnya dan jadikan itu pangkat bilangan basi 10 nya.
a. 1.000 = 10^3
b. 100.000 = 10^5
c. 1.000.000 = 10^6
d. 10.000.000 = 10^7
Soal 5
Nyatakan bilangan berikut dalam perpangkatan dengan basir 2
a. 256
b. 64
c. 512
d. 1.048.576
Jawab :
Caranya adalah dengan mengubah angka – angka diatas menjadi perkalian berulang 2, kemudian baru kita buat bilangan perpangkatannya.
a. 256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 28
b. 64 = 2 x 2 x 2 x 2 x 2 x 2 = 26
c. 512 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 = 29
d. 1.048.576 = 512 x 512 x 4 = 29 x 29 x 22 = 29 + 9 + 2 = 220
Soal 6 :Menentukan operasi campuran bilangan berpangkat
Tentukanlah hasil dari operasi berikut ini.
a. 5 + (3 x 2^4)
b. ½ (6^3 – 4^2)
c. 8 + (3 x (-3)^4)
d. (6^4 – 4^4) : 2
e. (1/4)^4 x (-1/3)^2
Jawab :
Yang perlu kalian ingat dalam aturan operasi bilangan adalah operasi mana yang dikerjakan terlebih dahulu. Urutannya adalah sebagai berikut:
1. Dalam kurung
2. Akar dan pangkat
3. Kali dan bagi
4. Tambah dan kurang
a. 5 + 3 x 2^4 = 5 + 3 x 16 = 5 + 48 = 53
b. ½ (6^3 – 4^2) = ½ (216 – 8) = ½ (208) = 104
c. 8 + 3 x (-3)^4 = 8 x 3 x 81 = 1944
d. (6^4 – 4^4) : 2 = (1296 – 256) : 2 = 1040 : 2 = 520
e. (1/4)^4 x (-1/3)^2 = (1/4^4 ) x (1/3^2 ) = 1/256 x 1/9 = 1/2304
Soal 8 : Menentukan pangkat yang sesuai dari suatu persamaan bilangan berpangkat
a. 7^x = 343
b. 2^x = 64
c. 10^x = 10.000
d. 5^x = 625
Jawab :
Jika :
a^x = a^y maka x = y
Contoh : 2^x = 8, berapa nilai x?
Jawab : 2^x = 2^3 ==> maka x = 3
a. 7^x = 343 ==> 7^x = 73 ==> x = 3
b. 2^x = 64 ==> 2^x = 26 ==> x = 6
c. 10^x = 10.000 ==> 10^x = 104 ==> x = 4
d. 5^x = 625 ==> 5^x = 54 ==> x = 4


Posting Komentar untuk "Tutorial Menjawab Soal Matematika Kelas 9 SMP - Aturan Dasar Bilangan Berpangkat"