Tutorial Menjawab Soal Tentang Operasi Penjumlahan, Pengurangan, dan Perkalian Bentuk Aljabar
Soal 1
Sederhanakanlah bentuk aljabar berikut.
a. 9p – 4 + (-3p) + 8
b. 2m + 5mn + (-12m) – 13mn
c. 3a^2 + 5ab – 9 – a^2 + 3ab – 6
d. 6x^2 – 12xy + 20y – 6x^2 + 7xy – 2y
Jawab :
Menyederhanakan bentuk aljabar yang emngandung operasi penjumlahan dan pengurangan artinya adalah menjumlahkan atau mengurangkan suku – suku aljabar yang sejenis. Ingat bahwa hanya suku sejenislah yang bisa kita jumlahkan atau kurangkan.
a. 9p – 4 + (-3p) + 8
Suku – suku sejenis:
9p dan – 3p
-4 dan 9
Langkah pertama kelompokkan suku – suku sejenis itu menjadi berdekatan terlebih dahulu.
= 9p – 4 + (-3p) + 8
= 9p + (-3p) – 4 + 8 (+ (-3p) = - 3p)
= 9p – 3p – 4 + 8 (9p – 3p = 6p dan – 4 + 8 = 4)
= 6p + 4
b. 2m + 5mn + (-12m) – 13mn
Suku – suku sejenis :
2m dan – 12m
5mn dan – 13mn
= 2m + 5mn + (-12m) – 13mn
= 2m + (-12m) + 5mn – 13mn
= 2m – 12m + 5mn – 13mn
= – 10m 8mn
c. 3a^2 + 5ab – 9 – a^2 + 3ab – 6 = 3a^2 – a^2 + 5ab + 3ab – 9 – 6
= 2a^2 + 8ab – 15
d. 6x^2 – 12xy + 20y – 6x^2 + 7xy – 2y = 6x^2 – 6x^2 – 12xy + 7xy + 20y – 2y
= - 5xy + 18 y
Soal 2
Nyatakan hasil perkalian bentuk aljabar berikut sebagai jumlah atau selisih.
a. -2(a – 2b + 10)
b. xy(y^2 – 6)
c. -2p(p^2 – 3)
Jawab :
Jika terdapat operasi berikut :
–( a) = - a, Contoh : - 2 (3a) = - 6a
–( - a) = a, Contoh : - 2(- 3a) = 6a
+ ( - a) = -a, Contoh : 2( -3a) = - 6a
Jika kita akan membuka kurung aljabar, jika tanda didepanya negatif ( - ), maka akan terdapat pengalian tanda seperti di bawah ini :
a. -2(a – 2b + 10) = -2a + 4b -10
b. xy(y^2 – 6) = xy^3 – 6xy
c. -2p(p^2 – 3) = -2p^3 + 6p
Soal 3
Sederhanakanlah bentuk ajabar berikut :
a. 2( - 5a – 2b) – 7a + 2b
b. 4(3m^3 – 8m^2 + m) – 5(m^3 + m^2 – 7m)
Jawab :
a. 2( - 5a – 2b) – 7a + 2b
Maka penyederhanaannya menjadi :
2( - 5a – 2b) – 7a + 2b = (-10a – 4b) – 7a + 2b
= - 10a – 7a – 4b + 2b
= - 17a – 2b
b. 4(3m^3 – 8m^2 + m) – 5(m^3 + m^2 – 7m)
4(3m^3 – 8m^2 + m) = (4.3m^3) + (4.-8m^2) + (4.m)
= 12m^3 + (-32m^2) + 4m
= 12m^3 – 32m^2 + 4m
5(m^3 + m^2 – 7m) = (5.m^3) + (5.m^2) – (5. -7m)
= 5m^3 +5m^2 – (- 35m)
= 5m^3 + 5m^2 + 35m
Maka penyederhanaannya menjadi :
Soal 4
Nyatakan bentuk aljabar berikut sebagai perkalian konstanta dengan bentuk aljabar!.
a. 5x – 15y
b. -2p + q – 3r
c. 3x^2 + 9xy – 18xy^2
Jawab :
Agar memahami maksud soal, saya contohkan option a dengan detail.
5x – 15y
Menurut kalian ada tidak yang sama antara suku 5x dengan – 15y. jika kalian jeli, ternyata salah satu faktor kedua koefisien suku aljabar tersebut ada yang sama.
5x – 15 y bisa kita tulis = (5 .1)x – (5.3)y
Karena 5 adalah faktor yang sama antara kedua suku aljabar tersebut, maka bisa kita keluarkan. Jadinya seperti ini :
= 5x – 15 y
= (5 .1)x – (5.3)y
= 5 (x – 3y)
Nah itulah bentuk perkalian konstanta dengan bentuk aljabar seperti yang dimaksud pada perintah soal.
b. -2p + q – 3r
Jika kita perhatikan suku – suku bentuk ajabar ini, ternyata tidak ada yang sama faktornya sehingga tidak usah kita sederhanakan. Bentuk aljabar ini sudah yang paling sederhana.
d. 3x^2 + 9xy – 18xy^2 = 3 . x . x + 3 . 3 . x . y – 3 . 6 . x . y . y
Dari penjebaran diatas akan dapat kita lihat bahwa ketiga suku pada bentuk alhabar diatas memiliki kesamaan yaitu faktor 3 dan x, tetapi karena yang diminta adalah perkalian konstanta, sehingga angka 3 saja yang harus kita keluarkan.
3x^2 + 9xy – 18xy^2 = 3 . x . x + 3 . 3 . x . y – 3.6 . x . y . y
= 3 (x.x+ 3.x.y – 6.x.y.y)
= 3 (x^2 + 3xy – 6xy^2)
Soal 5
Tentukanlah hasil perkalian suku dua bentuk aljabar berikut.
a. (x + 2) (x – 3)
b. (3 – a) (5 + a)
Jawab :
Untuk menyelesaikan soal diatas, kita bisa menggunakan dua cara yaitu :
a. (x + 2) (x – 3)
1. Menggunakan sifat distributif
2. Dengan skema
Dengan cara yang sama, kalian tentu bisa mengerjakan soal option b bukan! Ayo kerjakan sendiri.
Nah, sekian tutorial singkat mengenai cara menjawab soal operasi penjumlahan. Pengurangan dan perkalian bentuk aljabar. Jika kalian punya pertanyaan yang tidak bisa kalian mengerti, bisa tuliskan di kolom komentar.
Sederhanakanlah bentuk aljabar berikut.
a. 9p – 4 + (-3p) + 8
b. 2m + 5mn + (-12m) – 13mn
c. 3a^2 + 5ab – 9 – a^2 + 3ab – 6
d. 6x^2 – 12xy + 20y – 6x^2 + 7xy – 2y
Jawab :
Menyederhanakan bentuk aljabar yang emngandung operasi penjumlahan dan pengurangan artinya adalah menjumlahkan atau mengurangkan suku – suku aljabar yang sejenis. Ingat bahwa hanya suku sejenislah yang bisa kita jumlahkan atau kurangkan.
a. 9p – 4 + (-3p) + 8
Suku – suku sejenis:
9p dan – 3p
-4 dan 9
Langkah pertama kelompokkan suku – suku sejenis itu menjadi berdekatan terlebih dahulu.
= 9p – 4 + (-3p) + 8
= 9p + (-3p) – 4 + 8 (+ (-3p) = - 3p)
= 9p – 3p – 4 + 8 (9p – 3p = 6p dan – 4 + 8 = 4)
= 6p + 4
b. 2m + 5mn + (-12m) – 13mn
Suku – suku sejenis :
2m dan – 12m
5mn dan – 13mn
= 2m + 5mn + (-12m) – 13mn
= 2m + (-12m) + 5mn – 13mn
= 2m – 12m + 5mn – 13mn
= – 10m 8mn
c. 3a^2 + 5ab – 9 – a^2 + 3ab – 6 = 3a^2 – a^2 + 5ab + 3ab – 9 – 6
= 2a^2 + 8ab – 15
d. 6x^2 – 12xy + 20y – 6x^2 + 7xy – 2y = 6x^2 – 6x^2 – 12xy + 7xy + 20y – 2y
= - 5xy + 18 y
Soal 2
Nyatakan hasil perkalian bentuk aljabar berikut sebagai jumlah atau selisih.
a. -2(a – 2b + 10)
b. xy(y^2 – 6)
c. -2p(p^2 – 3)
Jawab :
Jika terdapat operasi berikut :
–( a) = - a, Contoh : - 2 (3a) = - 6a
–( - a) = a, Contoh : - 2(- 3a) = 6a
+ ( - a) = -a, Contoh : 2( -3a) = - 6a
Jika kita akan membuka kurung aljabar, jika tanda didepanya negatif ( - ), maka akan terdapat pengalian tanda seperti di bawah ini :
a. -2(a – 2b + 10) = -2a + 4b -10
b. xy(y^2 – 6) = xy^3 – 6xy
c. -2p(p^2 – 3) = -2p^3 + 6p
Soal 3
Sederhanakanlah bentuk ajabar berikut :
a. 2( - 5a – 2b) – 7a + 2b
b. 4(3m^3 – 8m^2 + m) – 5(m^3 + m^2 – 7m)
Jawab :
a. 2( - 5a – 2b) – 7a + 2b
Maka penyederhanaannya menjadi :
2( - 5a – 2b) – 7a + 2b = (-10a – 4b) – 7a + 2b
= - 10a – 7a – 4b + 2b
= - 17a – 2b
b. 4(3m^3 – 8m^2 + m) – 5(m^3 + m^2 – 7m)
4(3m^3 – 8m^2 + m) = (4.3m^3) + (4.-8m^2) + (4.m)
= 12m^3 + (-32m^2) + 4m
= 12m^3 – 32m^2 + 4m
5(m^3 + m^2 – 7m) = (5.m^3) + (5.m^2) – (5. -7m)
= 5m^3 +5m^2 – (- 35m)
= 5m^3 + 5m^2 + 35m
Maka penyederhanaannya menjadi :
Soal 4
Nyatakan bentuk aljabar berikut sebagai perkalian konstanta dengan bentuk aljabar!.
a. 5x – 15y
b. -2p + q – 3r
c. 3x^2 + 9xy – 18xy^2
Jawab :
Agar memahami maksud soal, saya contohkan option a dengan detail.
5x – 15y
Menurut kalian ada tidak yang sama antara suku 5x dengan – 15y. jika kalian jeli, ternyata salah satu faktor kedua koefisien suku aljabar tersebut ada yang sama.
5x – 15 y bisa kita tulis = (5 .1)x – (5.3)y
Karena 5 adalah faktor yang sama antara kedua suku aljabar tersebut, maka bisa kita keluarkan. Jadinya seperti ini :
= 5x – 15 y
= (5 .1)x – (5.3)y
= 5 (x – 3y)
Nah itulah bentuk perkalian konstanta dengan bentuk aljabar seperti yang dimaksud pada perintah soal.
b. -2p + q – 3r
Jika kita perhatikan suku – suku bentuk ajabar ini, ternyata tidak ada yang sama faktornya sehingga tidak usah kita sederhanakan. Bentuk aljabar ini sudah yang paling sederhana.
d. 3x^2 + 9xy – 18xy^2 = 3 . x . x + 3 . 3 . x . y – 3 . 6 . x . y . y
Dari penjebaran diatas akan dapat kita lihat bahwa ketiga suku pada bentuk alhabar diatas memiliki kesamaan yaitu faktor 3 dan x, tetapi karena yang diminta adalah perkalian konstanta, sehingga angka 3 saja yang harus kita keluarkan.
3x^2 + 9xy – 18xy^2 = 3 . x . x + 3 . 3 . x . y – 3.6 . x . y . y
= 3 (x.x+ 3.x.y – 6.x.y.y)
= 3 (x^2 + 3xy – 6xy^2)
Soal 5
Tentukanlah hasil perkalian suku dua bentuk aljabar berikut.
a. (x + 2) (x – 3)
b. (3 – a) (5 + a)
Jawab :
Untuk menyelesaikan soal diatas, kita bisa menggunakan dua cara yaitu :
a. (x + 2) (x – 3)
1. Menggunakan sifat distributif
2. Dengan skema
Dengan cara yang sama, kalian tentu bisa mengerjakan soal option b bukan! Ayo kerjakan sendiri.
Nah, sekian tutorial singkat mengenai cara menjawab soal operasi penjumlahan. Pengurangan dan perkalian bentuk aljabar. Jika kalian punya pertanyaan yang tidak bisa kalian mengerti, bisa tuliskan di kolom komentar.

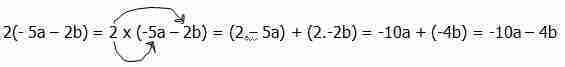


Posting Komentar untuk "Tutorial Menjawab Soal Tentang Operasi Penjumlahan, Pengurangan, dan Perkalian Bentuk Aljabar"