Tutorial Menjawab Soal Matematika {Pilihan Ganda} Kelas 8 SMP Materi Memahami Bentuk Penyajian Fungsi

Di dalam postingan kali ini terdapat 8 contoh soal matematika dalam bentuk pilihan ganda tentang penyajian fungsi beserta pembahasannya.

Soal-soal di bawah ini dibuat sedemikian rupa sehingga mirip dengan soal-soal yang terdapat dalam buku matematika SMP semester 1 kelas 8 bab fungsi. Oleh karena itulah soal-soal ini sangat cocok digunakan baik sebagai media latihan maupun untuk bahan evaluasi belajar bagi siswa di sekolah. Nah berikut adalah soal-soalnya.

Contoh Soal 1

Fungsi dari himpunan A ke himpunan B jika dinyatakan dengan himpunan pasangan berutan adalah sebagai berikut:

f (A ke B) = {(1, 3), (2, 4), (3, 5), (4, 6), (5, 7)}

Domain untuk fungsi tersebut adalah……..

A. {1, 2, 3, 4, 5}

B. {3, 4, 5, 6, 7}

C. {1, 2, 3, 4}

D. {3, 4, 5, 6}

Pembahasan:

Domain atau daerah asal untuk fungsi dari himpunan A himpunan B adalah seluruh anggota himpunan A. Kalau fungsi berarti setiap anggota himpunan A telah memilih tepat 1 anggota himpunan B.

Jadi jawaban untuk soal di atas adalah yang opsi A. 

Kalau kodomain atau daerah lawan tidak bisa kita tentukan hanya dari melihat himpunan pasangan berurutan di atas. Karena, daerah lawan adalah seluruh anggota himpunan B, baik yang berpasangan dengan anggota himpunan A maupun yang tidak berpasangan.

Kunci Jawaban: A

Contoh Soal 2

Diketahui dua buah himpunan sebagai berikut

Himpunan C = {5, 6, 7, 8} 

Himpunan D = {9, 10, 11, 12, 13, 14  15, 16}

Jika relasi yang menghubungkan fungsi dari himpunan C ke himpunan D adalah "setengah dari", maka diagram panah di bawah ini yang benar menunjukkan fungsi tersebut adalah………..

Pembahasan:

Untuk menjawab soal di atas langkah pertama yang harus kita lakukan adalah menentukan pasangan dari fungsi himpunan C dan D yang dihubungkan oleh relasi "setengah dari"

5 setengah dari 10

6 setengah dari 12

7 setengah dari 14

8 setengah dari 16

Selanjutnya barulah kita buat diagram panah yang menghubungkan masing-masing pasangan di atas. Hasilnya adalah sebagai berikut.

Kunci Jawaban: D

Contoh Soal 3

Perhatikan tabel dibawah ini!

Berdasarkan tabel diatas maka rumus dari fungsi tersebut adalah……….

A. f(x) = 3x

B. f(x) = ⅓x 

C. f(x) = 2x

D. f(x) = ½x 

Pembahasan:

Untuk menentukan rumus fungsi, perhatikanlah penjelasan berikut.

Rumus umum suatj fungsi:

f(x) = ax + b

Kita akan cari nilai a dan b tersebut. Ambil dua buah data dari tabel diatas.

Data 1 = x = 6 dan f(x) = 2

f(x) = ax + b

f(6) = ax + b

2 = a.6 + b

6a + b = 2……persamaan 1

Data 2 = x = 9 dan f(x) = 3

f(x) = ax + b

f(9) = ax + b

3 = a.9 + b

9a + b = 3……persamaan 2

Eliminasi persamaan 1 dan 2 untuk mencari nilai a.

6a + b = 2

9a + b = 3 

-3a = -1

a = ⅓

Mencari nilai b. Masukkan nilai a = ⅓ ke salah satu persamaan.

6a + b = 2

6.⅓ + b = 2

2 + b = 2

b = 2 - 2

b = 0

Maka, rumus fungsi berdasarkan tabek diatas adalah:

f(x) = ax + b = ⅓x + 0 = ⅓x

Jadi, rumus untuk fungsi tersebut adalah f(x) = ⅓x

Kunci Jawaban: B

Contoh Soal 4

Berdasarkan contoh soal nomor 3, nilai dari f(x) saat x = 72 adalah……… 

A. 32

B. 24

C. 16

D. 12

Pembahasan:

Rumus fungsi yang diperoleh dari soal nomor 3 adalah f(x) = ⅓x 

Jika x = 72, maka:

f(x) = ⅓ . 72 = 24

 

Kunci Jawaban: B

Contoh Soal 5

Fungsi dari suatu himpunan ke himpunan yang lain dinyatakan dengan rumus fungsi f(x) = 2x + 1. Jika domain dari fungsi tersebut adalah (2, 4, 6, 8}, maka daerah hasil atau range untuk fungsi tersebut adalah………

A. {5, 9, 13, 17}

B. {6, 10, 14, 18}

C. {5, 7, 9, 11}

D. {9, 13, 17, 21}

Pembahasan:

Cara menjawab soal di atas sangatlah mudah. Untuk mencari daerah hasil masukkan lah masing-masing nilai dari daerah asal ke rumah fungsi yang diberikan.

f(2) = 2.2 + 1 = 5

f(4) = 2.4 + 1 = 9

f(6) = 2.6 + 1 = 13

f(8) = 2.8 + 1 = 17

Jadi daerah hasil atau range dari fungsi tersebut adalah {5, 9, 13, 17}.

Kunci Jawaban: A

Contoh Soal 6

Fungsi dari himpunan P ke himpunan Q dinyatan oleh rumus f(x) = 4x - 3. Jika anggota dari himpunan P adalah {1, 3, 5, 7, 9, 11), maka tabel di bawah ini yang paling tepat digunakan untuk menyajikan fungsi tersebut adalah……….

Pembahasan:

Karena pada soal diketahui rumus fungsi dari himpunan P himpunan Q, maka seluruh anggota dari himpunan P merupakan daerah asal atau domain. Karena merupakan fungsi berarti setiap anggota dari himpunan P ini harus besar pasangan dengan tepat satu anggota himpunan Q.

Oleh karena itu kita cari daerah hasilnya terlebih dahulu dengan memasukkan masing-masing anggota himpunan P sebagai x ke dalam rumus fungsi.

f(1) = 4.1 - 3 = 1

f(3) = 4.3 - 3 = 9

f(5) = 4.5 - 3 = 17

f(7) = 4.7 - 3 = 25

f(9) = 4.9 - 3 = 33

f(11) = 4.11 - 3 = 41

Daerah hasilnya adalah {1, 9, 17  25, 33}. Situ tinggal buat deh tabelnya. Hasilnya adalah sebagai berikut.

Berdasarkan tabell diatas maka jawaban untuk soal ini yang benar adalah yang opsi B. 

Kunci Jawaban: B

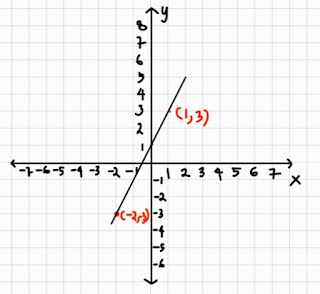
Grafik di bawah ini digunakan untuk menjawab contoh soal nomor 7 dan 8

Contoh Soal 7

Rumus fungsi berdasarkan grafik diatas adalah…….

A. x + 1

B. 2x - 1

C. x + 2

D. 2x + 1

Pembahasan:

Kalau kita lihat grafik di atas, terdapat dua buah titik yang dilaluinya yaitu:

(-2,-3)

(1, 3)

Dari titik pertama dapat kita katakan bahwa jika nilai x = -2, maka f(-2) = y = -3. Kita tahu bahwa persamaan umum untuk rumus fungsi adalah sebagai berikut.

f(x) = ax + b

f(-2) = -2a + b

-3 = -2a + b…….persamaan 1

Sedangkan dari titik kedua dapat kita katakan bahwa jika nilai x = 1, maka f(1) = y = 3.

f(x) = ax + b

f(1) = a + b

3 = a + b……..persamaan 2

Dengan mengeliminasi persamaan 1 dan persamaan 2 kita bisa memperoleh nilai a.

-2a + b = -3

a + b = 3

-3a = -6

a = 2

Untuk mencari B masukkan nilai a = 2 ke persamaan 2 ( boleh juga persamaan satu, terserah kalian mau pilih yang mana).

a + b = 3

b = 3 - a = 3 - 2 = 1

Jadi rumus fungsi untuk grafik di atas adalah:

f(x) = ax + b 

f(x) = 2x + 1

Kunci Jawaban: D

Contoh Soal 8

Berdasarkan rumus fungsinya, maka nilai dari f(5), f(6) dan f(7) berturut-turut adalah……..

9, 11, 13

11, 13, 15

13, 15, 17

15, 17, 19

Pembahasan:

Dari soal sebelumnya kita sudah dapatkan rumus fungsi yaitu f(x) = 2x + 1. Berarti:

f(5) = 2.5 + 1 = 11

f(6) = 2.6 + 1 = 13

f(7) = 2.7 + 1 = 15

Jadi nilai ketiganya berturut-turut adalah 11 13 dan 15.

Kunci Jawaban: A

Nah itulah 8 contoh soal matematika SMP dalam bentuk pilihan ganda mengenai penyajian fungsi yang dapat saya bagikan pada artikel kali ini. Semoga soal-soal di atas bermanfaat bagi kamu yang telah berkunjung ke blog ini ya. Sampai jumpa lagi di artikel lainnya.

Note;

Artikel ini telah diperbaharui pada tanggal 8 Agustus 2023 dengan mengubah seluruh soal menjadi bentuk pilihan ganda. 

Location:

Berbagi :